If classical physics is the science of the everyday Universe and relativity is the science of high speeds and intense gravity, then quantum physics is the science of the extremely tiny.
However, unlike relativity, quantum physics didn’t primarily originate from one person’s contributions. Instead, it’s the result of many physicists sharing ideas and experimenting cumulatively over more than a century. Unfortunately, this same lack of centrality has also led to tremendous complexity in both the theories themselves and the amount of misinformation and even mysticism around them. So the real reason “no one understands quantum physics” isn’t because it’s unlearnable, but rather because it’s so difficult to convey digestible information on the subject while still being accurate…
I think there are two villains here: (1) Physicists, who are (rightly) desperate to explain to the world the extraordinary, fascinating, and profound implications of quantum mechanics. But they are afraid of intimidating an audience that gags at the sight of an equation; they want to convey the excitement without the substance. So they resort to forced similes and grossly misleading metaphors (quantum tunneling means you can walk through walls—somehow it never works when I try it). (2) Non-physicists who are intrigued by words like “uncertainty” and “indeterminacy,” but are too lazy to do the serious work it takes to understand them.
David J. Griffiths
With this challenge in mind, I’ve labored to do the work outlining modern quantum physics in simplified question and answer format, while not going so easy on the reader as to rob them of a genuinely good understanding of the concepts.
First, I’ll briefly touch on discrete quantization. Then we’ll summarize the basics of wave-particle duality and dive into specific questions and answers one at a time.
Discrete Quantization
As mentioned earlier, the smallest of the small in the Universe, as far as possible states of energy are concerned anyway, aren’t continuous. They’re basically a bunch of either-ors that cannot be further subdivided. You can have a “1” or a “2,” for example, but never something between a one or two.
Think of the stairs in a building vs. a wheelchair ramp. That’s how the Universe operates fundamentally – just like stairs.
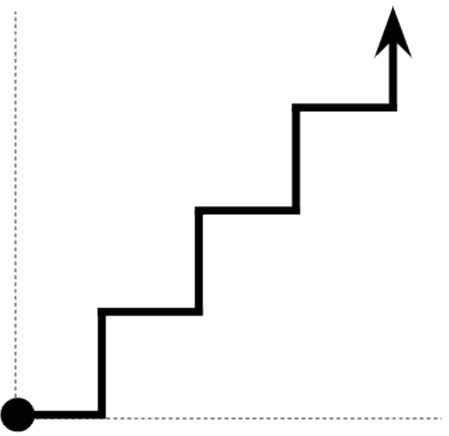
This is a much bigger deal than it may seem and the implications of quantization deserve an entire post of their own, so I’ll talk in more detail about these ramifications (and how we know energy is quantized) in a future publication. For now, let’s accept that all modern experimental evidence indicates we live in a quantized Universe.
Wave-Particle Duality
I like to think of wave-particle duality as the “meat and potatoes” of quantum theory. It starts with some re-education…
Many of us were taught that matter is made up of tiny cannon balls called “atoms.” This idea isn’t new. The contrary, in fact – the first known theory of an atomized Universe came from the Greek philosopher Democritus around the 5th century BC. And prior to the 20th century, classical physics also held that matter exists as “particles” and light exists as “waves,” and that was that!
But this understanding of our Universe is wrong. The reality of our Universe is far more bizarre than we could have known: We’ve learned from experimentation that what we know as “matter” is not a particle at all. Nor is it a wave. It’s both! At the same time! But how can something be both one thing and the other? You can’t have a toaster that is also a fish, right?
Well, sort of.
It turns out on quantum scales things can exhibit the properties of both particles and waves simultaneously because what we are perceiving as “particles” are actually just waves themselves. And ultimately, all waves and particles can be described in terms of three-dimensional “fields.”
The below figures should help you begin to visualize waves, particles, and fields:
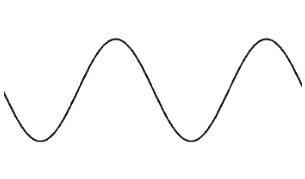
Wave (Sinusoid): A disturbance that transfers energy through matter or space.
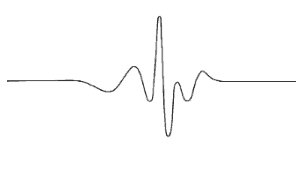
Particle (Wave Packet): A short “burst” or “pulse” of wave action derived from many component waves.
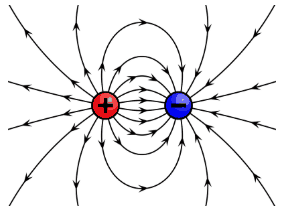
Field: A useful mathematical representation of a body exerting “action at a distance” through three-dimensional space via electromagnetism, gravity, particles, etc. (measured via scalars, vectors, and tensors). For our purposes here, a field can simply be thought of as what waves are like in three dimensions.
Here’s the takeaway: All matter and energy in the Universe is a wave or some combination of waves, such as particles (wave packets) and fields (three-dimensional waves).
When we define a particle, we’re referring to a wave packet. When we define a wave, we’re referring to a sinusoid. Each of these has specific properties: A particle has a high degree of certainty regarding it’s position, but a low degree of certainty regarding its momentum (motion). A wave has a low degree of certainty regarding it’s position, but a high degree of certainty regarding its momentum.
For example: We know a particle’s location, but not how it’s moving. We know how a wave is moving, but not it’s location.
It’s important to know that you can’t have complete certainty of both position and momentum at the same time, which is known as the “Uncertainty Principle.” In fact, handling uncertainty is the primary foundation of all of quantum physics. We use fancy mathematical concepts like “wave functions” (\Psi) and “probability amplitudes” to describe this uncertainty of matter and energy.
For example, here’s the Schrödinger Equation mentioned in the earlier timeline (which is about as important to quantum physics as Newton’s laws of motion are to classical physics):
H(t)|\Psi(t)\rangle=i\hbar\frac{\partial}{\partial t}|\Psi(t)\rangle
But it’s not quite so simple… (little math joke).
The reality is three-dimensional space still applies on quantum scales, so we need to account for how particles and waves behave in those terms and not just in the two-dimensional depictions of waves, particles, and fields above. This is the reason math like the Schrödinger Equation was developed. It allows us to represent the probability of finding a particle in four-dimensional space (an electron in its orbital, for example). The graphical depictions of electron orbitals around hydrogen nuclei you see below are derivatives of this math, in fact.
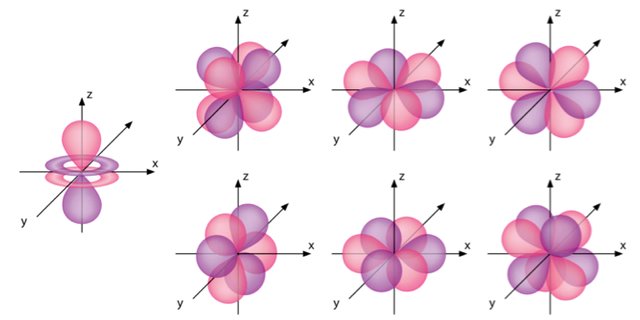
These ideas and others build up to “Quantum Field Theory (QFT),” which is the newest frontier-science in our understanding of the physics of the very small. In QFT (and QM), we move away from well-defined classical ideas and begin using esoteric maths to describe what’s actually happening. Confusing as this is, this field of science is incredibly precise in predicting what will happen on larger scales. And since we can’t see, hear, touch, smell, or taste the quantum world, this math was developed to give us a sort of “6th sense” to calibrate our thinking to the reality of our Universe.
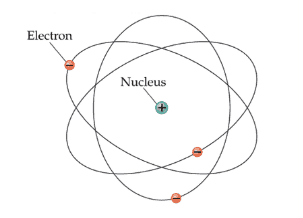
A great example of this calibration is our updated understanding of the atom. In the figures below, the picture on the left represents how most folks learned about atoms. However, this depiction of the atom really only works within classical physics and quickly breaks down in the quantum arena (it’s wrong). A more realistic graphic is on the right: Electrons don’t have singular defined positions like you see on the left, rather they have many. In fact, due to the uncertainty of its infinite different possible positions, we must conclude the electron is in a “superposition” of all of those states simultaneously; that it doesn’t have any defined position. It’s only when we measure the location of the electron that it appears to be in one spot (I’ll go into far more depth on this below – stay strong!).
That tiny dot you see in the center of the picture on the right is the nucleus of the atom, which is some combination of protons and/or neutrons. These protons and neutrons themselves are probability fields, albeit fields of much lesser volume.

Again, this boils down to the following: All matter and energy in the Universe is a wave or some combination of waves, such as particles (wave packets) and fields (three-dimensional waves).
Lost? A lot to absorb? That’s okay! Just know there’s nothing magical about how any of this works. It’s just math we created that agrees with and predicts real world experimentation. But simply telling you that won’t do. Let’s break these concepts into bite-sized chunks with some Q&A:
Why can’t we just use a microscope to see what’s happening on quantum scales?
Because light doesn’t behave the way you think it should down there.
“Optics” is the science of sight and the behavior of light. We know from optics that visible light has a wavelength (distance between crests or troughs of the waves) ranging from 380 nanometers (far left of the above picture) to 740 nanometers (far right). A subatomic particle is much, much smaller than 380 nanometers. In order for visible light to reflect off of the object it’s interacting with, that object must have a diameter greater than 380 nanometers. This means visible light is useless on scales below 380 nanometers.
But that doesn’t mean we can’t use light beyond the visible spectrum!
As you can see in the image below, we can move to the left on the broader electromagnetic spectrum of light to decrease wavelength to the point where we can get useful information from bouncing light off a particle. In particular, we can use X-rays (<10 nanometers) or even gamma rays (<10 picometers) to gain resolution on tiny quantum objects.
However, the problem with this method is light with smaller wavelengths carries much more energy. So it’s like shooting bullets at a piece of paper to read the braille imprinted on it. The bullets will be deflected by the braille barely detectably (but measurably), while the paper itself will be destroyed in the process. This brings us to our next question…
What does “observer” really mean in physics? The “observer effect?”
An observer is anything or anyone whose state is dependent on the thing being observed. An observer could be a human, sure. But it could also be a spectrophotometer (a machine that measures the wavelength of light), a Geiger counter (a machine that measures radiation), or even a lump of coal. An observer doesn’t have to be alive or even have a purpose. It can be anything that is thermodynamically dependent on the thing being observed (we’ll cover thermodynamics in more detail in a later post).
The “observer effect” is the idea that the observer necessarily interacts with (and thus changes) the thing being observed by observing it. It’s a true statement, but there’s a lot of froo froo science-fiction nonsense around this idea (a.k.a. “Quantum Woo”).
As we just discussed when we talked about light, the reality is when you’re operating on a quantum scale it’s impossible to prevent yourself from disturbing what you’re trying to measure. This is because out of all of our senses, the only one that “works” on the quantum scale is our vision… sort of. In order to “see” what’s going on, we must bounce higher frequency radiation (or other things like electrons) off of what we’re measuring. This means we are physically interacting with these quantum objects by literally hitting them with stuff, so of course there’s an observer “effect.” It’s rather unavoidable when you’re literally smacking the thing you’re measuring!
The froo froo nonsense comes in when people try to imply there’s some unexplainable magic at work here; that the thing being observed “knows” it’s being watched and acts of its own volition. One of the more wrong and unfortunately widespread ideas is that quantum particles are reacting to the “consciousness” of the observer. This is incorrect, as the system will react regardless of who or what the observer is and whether or not they have consciousness.
In fact, the origin of the thinking that consciousness has something to do with quantum physics came from the (ridiculously intelligent) scientist John von Neumann and esteemed Eugene Wigner in the early 20th century via their Von Neumann–Wigner interpretation of quantum physics. What they were trying to wrap their heads around was eventually resolved via the discovery of “quantum decoherence” in the 1970s (don’t worry, we’ll cover what all these words mean below too).
The takeaway is you can reliably dismiss anyone’s opinion about quantum physics if the word “consciousness” is used as an explanation.
What is the “uncertainty principle?”
As we established, all matter and energy in the Universe is a wave or some combination of waves. The uncertainty principle simply describes what is knowable about those waves. It says that at any single point in time, it is impossible to know both the momentum and position of the wave (or wave packet) with absolute certainty.
Below is the equation describing this principle, where \sigma is standard deviation (a measure for the extent of uncertainty), x is position, p is momentum, and \hbar (“h bar”) is Planck’s reduced constant.
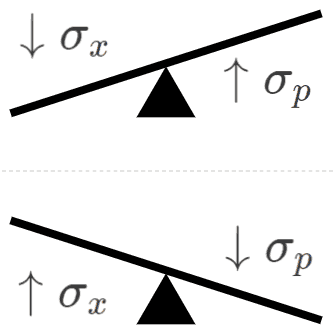
\sigma_x\sigma_p\geq\frac{\hbar}{2}
The equation above is an “inverse relationship” where decreasing x means p must increase proportionately to preserve Planck’s constant, and vice versa. This simply means that p and x are like a seesaw. If one goes down in uncertainty, the other must go up; there is a minimum uncertainty that must exist. If both sides of the seesaw went up to 100% certainty, the seesaw would break in half (which the Universe doesn’t allow, as it’s Planck’s “constant” and not Planck’s “maybe sometimes”):
Why is this? Why must a certain amount of uncertainty exist in every quantum object at all times? Well, it comes down to how waves work on quantum scales. And unless you’re a mathematician, the best way for me to describe this is with pictures.
So here’s what 100% certainty about a wave’s momentum looks like (meaning we have zero certainty or complete uncertainty about the wave’s location – it’s everywhere!):
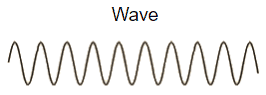
And here’s what high certainty about a wave’s position looks like:
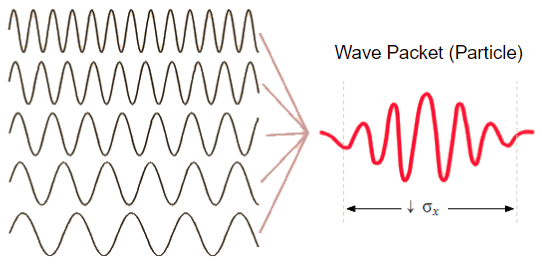
(Note that I said “high” instead of 100%, as 100% would infinitely compress the red wave packet (particle) into an infinitely thin and thus invisible vertical line, defeating the whole purpose of showing you what it looks like!)
Understanding the uncertainty principle can also help you understand how wave-particle duality could exist; as you can see in the above image, particles are simply a bunch of waves that make up a localized wave packet. And we generally know the location of wave packets, but not waves. Just as we can generally know the momentum of waves, but not wave packets. It’s a trade off!
Now it’s time to discuss what the uncertainty principle is not:
- The uncertainty principle is not a limitation in our technological ability to measure things
- The uncertainty principle is not “just math” or “just a theory”
- The uncertainty principle is not the same as the observer effect
The above misconceptions arise when folks are not grasping that the uncertainty of quantum waves is inherent to nature. It’s not just some mathematical artifact, it’s a very real thing that actually exists. For example, as an electron is in route, it’s precise location literally does not exist because it’s travelling in wave form. It only resolves into a wave packet (simultaneously losing certainty about it’s momentum) when it is measured (the observer effect). The quantum object literally transforms.
Interestingly, the uncertainty principle paired with the wave-nature of quantum reality is the fundamental reason we live in an indeterministic Universe. Even if you knew everything (and I mean everything), your ability to predict what happens next will still degrade proportional to the temporal distance of your prediction from your present time.
What does “superposition” mean?
If you toss a coin in the air there’s a 50-50 chance it will be heads or tails when you catch it. However, as it’s spinning in the air, it’s in a “superposition” of those two states. Until you catch the coin, it could go either way. That superposition “collapses” into heads or tails when you catch it and observe the result.
In principle, it’s really no different with an electron. Since uncertainty about the electron’s position is fundamental (the uncertainty principle), we are forced to assume it’s in all possible states simultaneously until we measure it (by smacking it – remember what I said above) and that uncertainty “collapses” into a more certain state.
What’s a wave function? A probability amplitude?
The wave function is simply math describing quantum systems in a state of superposition. It’s usually represented by the Greek letter \Psi (psi). The below equation is the differential “Schrödinger Equation” you saw earlier, which describes how the wave function “evolves” over time (causally, I might add). The wave function itself is actually just the solution to the Schrödinger Equation, which is expressed as something called a “probability amplitude” \Psi^2. A probability amplitude is just more math that describes the “probability cloud” of a quantum system’s properties (like the electron orbitals/clouds you saw earlier).
H(t)|\Psi(t)\rangle=i\hbar\frac{\partial}{\partial t}|\Psi(t)\rangle
On quantum scales, waves have many possible states. Because of the uncertainty principle, the precision of our knowledge is physically limited by the mechanics underlying how waves actually work in nature. So the wave function is ultimately just a mathematical tool that helps us measure the most likely characteristics of a quantum system; a sort of “compromise” where if we can’t know the exact properties of the system, we can at least know it’s most probable states.
Again, unless you’re an aspiring physicist or mathematician, don’t worry too much about understanding the esoteric math that drives the wave function. The important takeaway is it’s merely math invented to reliably model elementary particles.
Why can’t we see quantum effects in our everyday macro world?
As implied in the question, a quantum object like an electron behaves very differently than a baseball. For example, the electron will exhibit quantum properties such as wave-particle duality and superposition, where a baseball clearly does not. Why is this? Why don’t the things within our everyday experience exhibit these quantum behaviors? Aren’t they built from quantum particles? If every object we can see is composed of quantum particles, and quantum particles are fundamentally uncertain as outlined by the uncertainty principle, then shouldn’t the objects we see also exhibit uncertain behavior? And if we wait long enough (say, countless trillions of years), a brick of lead could have some ultra-tiny probability of suddenly turning into gold? Or a smartphone? Or a chicken? Etc.?
Sort of, but not really.
The reality is the uncertainty principle does not apply to anything beyond a single or small group a quantum objects, as it’s quickly averaged away as you continually add new quantum objects to the system.
Here’s why…
Say we poll 1,000 people to tell us their favorite color. In room A, 500 people are perfectly identical clones who all favor blue. In room B, there are 500 randomly chosen people off the streets of random cities around the world. What is the probability that every single person in room B chooses blue? Pretty low, right? What if we reduced the amount of people in room B to 2 people? What if we increased it to 100 thousand? Obviously, with 2 people in room B the odds are pretty good that they might choose the same color. But 100 thousand? No way.


Quantum systems are really no different than the two rooms in this analogy. Quantum behaviors only emerge in our macroscopic world when everyone (all the particles/waves) is picking the same “color.” This is known formally as a “coherent” system. Room A is an example of a coherent system. In fact, special quantum phenomena like superconductivity or superfluidity are due to objects being in a state of macroscopic-apparent “quantum coherence.” Room B, on the other hand, would be an example of “quantum decoherence.”
It’s important to note that not only does every individual quantum object have its own wavelength (“color”), but so does every group of quantum objects. These are known in aggregate as “matter waves.” As outlined below by the equation for the de Broglie wavelength (matter wave), \lambda “lambda” represents wavelength where h is Planck’s constant and p is momentum (remember, p=mv so anything with non-zero p contains energy; “stuff”).
\lambda=\frac{h}{p}
Basically, this means the more non-coherent quantum objects in a system, the more it’s aggregate matter wavelength will shrink. The below figure illustrates this compression.
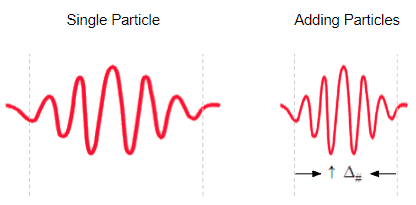
Quantum decoherence is an exponential process, so as you increase momentum (as you add non-coherent quantum objects to the system) very quickly you end up with an aggregate matter wave compressed to such an extreme that it can’t interact with other quantum waves the way a single electron could. This is the reason we don’t observe quantum behavior in classical systems (i.e. the apparently deterministic and classically newtonian world we experience).
So to make this a bit more digestible let’s ask the question again – why can’t we see quantum effects in the everyday world? Well, do you recall how unlikely 100 thousand people would be to pick the same color? Now, instead of 100 thousand, imagine trillions upon trillions of people all picking the same color, because that’s how many quantum objects are within even the tiniest visible grain of sand!
Although I can’t technically tell you there is zero chance that a quantum property will emerge from any decoherent object we can see with the naked eye, it would be unreasonably pedantic to differentiate that ridiculously tiny probability from zero, as no human can even comprehend how unlikely that would be (I mean this literally; we don’t have the physiological hardware to truly comprehend numbers on this scale).
However, I can tell you that there is indeed a zero probability of lead turning into gold, a smartphone, or a chicken over any amount of time. As it turns out, that violates the laws of conservation, which state energy cannot be created or destroyed and instead must be transformed.
What’s an eigenstate?
Now that you have a better understanding of quantum decoherence, you’ll have a much easier time understanding eigenstates. An “eigenstate” is simply the term we use to describe things that are sufficiently classical in nature. “Eigen” is a German word for “inherent” or “characteristic.” It’s a prefix we use to differentiate the uncertainty of quantum states from the certainty of “pinned down” (“Eigen”) classical states which have clear characteristics we can measure.
For example, since a grain of sand is in a classical state, it has known values for things like position and momentum, which we can label “eigenvalues” of position and momentum, respectively. However unlike the grain of sand, a quantum object like an electron has no eigenvalues of position or momentum because they are fundamentally uncertain.
There’s no black and white line in the sand between a quantum system and a classical system; it’s literally a transition directly relative to the decoherence of the system. The more decoherent it becomes, the more it approaches what we would call an “eigenstate.”
Long story short, if something’s in an eigen-something, we’re in the realm of classical physics.
What is quantum tunneling?
In classical physics, if you partition a pool of water with a plastic barrier, that water will stay partitioned forever unless energy is used to change the system. Quantum systems are very different. In the quantum world, a quantum object (a wave) is probabilistic. This means if you place a barrier in front of the quantum object, it won’t necessarily be trapped forever like the water. Instead, there is a non-zero probability the quantum object could ”tunnel” through the barrier.
Here’s what that looks like:
Classical Physics
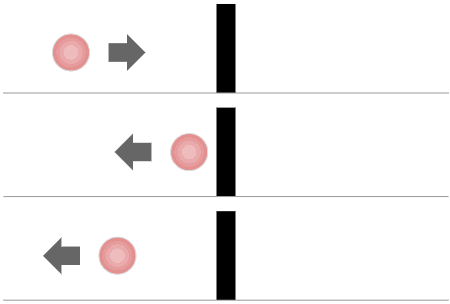
Quantum Physics
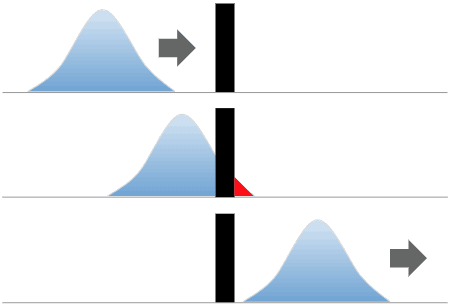
To more intuitively understand how this is possible, it’s important to recognize that both the quantum object and the barrier are composed of waves. The quantum barrier isn’t the same in principle as the classical plastic barrier that stops the water. In the classical world, you’re dealing with objects that have highly compressed wavelengths due to quantum decoherence, which are simply too small to extend their probability fields sufficiently. But in the quantum world that limitation doesn’t exist. As you can see in the image above, an electron’s wave function has a non-zero probability of placing the electron on the other side of the barrier.
Again, this is a very real phenomenon that actually happens. In fact, semiconductor components in computers such as the “tunneling diode” are possible only via quantum tunneling. Another great example is the electron scanning microscope, which uses the quantum tunneling between two charged surfaces to gain image resolution on objects far too small to see with conventional optical microscopes. Many technologies we enjoy today wouldn’t be possible without quantum tunneling – so much so that quantum tunneling is a major bedrock of evidence supporting the validity of modern quantum theory.
What is this “Schrödinger’s Cat” business all about?
Schrödinger’s Cat started out as a joke, but quantum physics isn’t a commonly understood subject so of course the media didn’t know any better and ran it as some iconic thought experiment. The reality is Erwin Schrödinger was simply satirizing the absurdity of quantum mechanics (particularly superposition and the wave function collapse). Scientists during the early 20th century had been trained from a young age to see the world through the lens of classical physics. To discover this time-tested paradigm was fundamentally wrong on quantum scales was a tough pill to swallow.
Here’s the thought experiment directly from Erwin Schrödinger himself:
One can even set up quite ridiculous cases. A cat is penned up in a steel chamber, along with the following device (which must be secured against direct interference by the cat): in a Geiger counter, there is a tiny bit of radioactive substance, so small, that perhaps in the course of the hour one of the atoms decays, but also, with equal probability, perhaps none; if it happens, the counter tube discharges and through a relay releases a hammer that shatters a small flask of hydrocyanic acid. If one has left this entire system to itself for an hour, one would say that the cat still lives if meanwhile no atom has decayed. The first atomic decay would have poisoned it. The psi-function of the entire system would express this by having in it the living and dead cat (pardon the expression) mixed or smeared out in equal parts.
Erwin Schrödinger
The irony behind this famous thought experiment is it isn’t even a good one! In fact, any quantum thought experiment that involves objects big enough to be visible to the human eye are destined to be inaccurate from the start. You simply can’t accurately describe the quantum world with macro examples because they are fundamentally different due to the uncertainty principle and quantum decoherence, which has been a big contributor to the general confusion of the public.
Ultimately however, the core problem behind Schrödinger’s Cat and other thought experiments like it (a problem which many respected physicists have been justifiably going a bit bonkers over historically) is the actual formalized mechanism behind the collapse of the wave function (i.e. what specifically caused it to collapse into this state rather than that state?). This mystery is formally known as the “measurement problem” in quantum physics and many quantum “interpretations” have arisen from brilliant people trying to propose how it could theoretically function. Although the measurement problem hasn’t technically been solved by consensus agreement, it’s become less and less of an issue today as quantum physics has gained resolution. But before we dive any further into the highly speculative interpretations of the measurement problem, we’ll need a very strong understanding of the experimental evidence we already have…
What is the double-slit experiment (DSE)?
The famous DSE is arguably the most important experiment in all of quantum theory. It’s been around for centuries, is repeatable and accessible to everyone, and has evolved concurrent with general technological advances. In its modern form, the DSE provides experimental evidence backing wave-particle duality, the uncertainty principle, and the probabilistic nature of the quantum Universe (it’s kind of a big deal).
Here’s how it works…
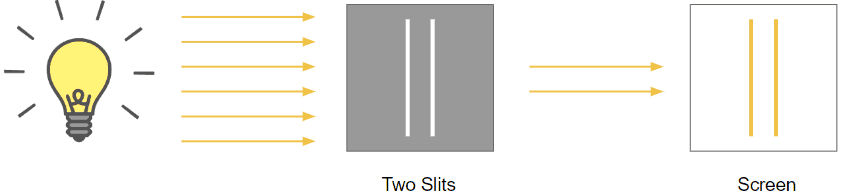
If you take a barrier and pierce two sufficiently thin vertical slits in it, then shine a light through said slits onto a screen, here’s what we expect to happen:
And here’s what actually happens:
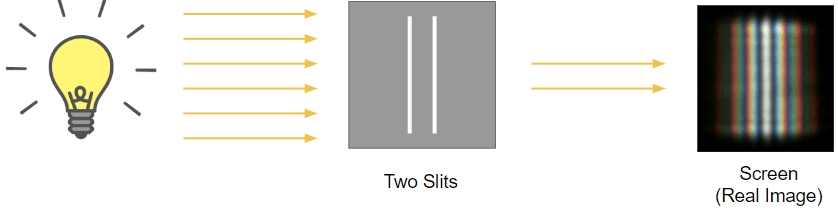
Why is this? Why did the two lines become many lines instead of just two? The answer lies in “wave interference,” which occurs when waves interact with each other (or even themselves) to create an “interference pattern.” This pattern is caused by waves interacting with each other “constructively” or “destructively” at intervals. You can actually observe this phenomenon at the beach when ocean waves intersect – some of the waves will remain and others will cancel out. What you’re seeing on the screen in the DSE is that same basic principle, which is how we know light is a wave.
Here’s a more intuitive diagram illustrating what’s happening:
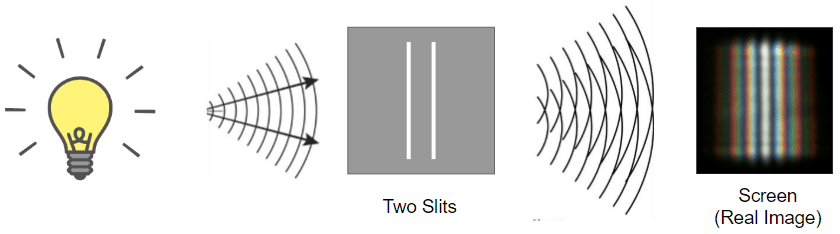
But this conclusion eventually presented problems.
By the early 20th century we had known light was a wave for a long time, but Max Planck’s radical discovery of the quantization of energy led Einstein to predict the quantization of light. Then, once Arthur Compton was able to support Einstein’s theory experimentally, we had our evidence that “photons” were genuinely particles too.
This new evidence gave the idea of light being a particle real validity in the scientific community and had a lot of extremely smart people scratching their heads. How can light be both a wave and a particle?
The next natural step was to begin testing the properties of isolated individual photons to see if we were missing something about their particle-nature. So we did! As technologies were developed, we became increasingly effective at isolating photons and firing them one at a time through the DSE. And here’s what we discovered:

In the image above, you can see that at first the individually fired photons appear random (left side). However, as we keep firing photons we eventually get the same wave interference pattern as before. How could a single particle be generating wave-interference?
Again, some extremely smart people were baffled by this.
As the quantum renaissance progressed, it was concluded that the only logical and possible explanation for these observations is that we were wrong: Light isn’t a particle or a wave, it’s literally both. And thus wave-particle duality was born.
Equations such as the Schrödinger Equation and it’s resulting wave functions were developed to map how this wave-particle duality could be possible. In the images below, you can actually “see” the computer-simulated wave function at work:

The brighter the white spot, the higher the probability you’ll find the particle in that location. As you can see, the single particle manages to travel through both slits simultaneously while still maintaining it’s wave-particle duality.
Interestingly, the simulation above isn’t limited to photons. It could equally be a simulation of an electron, as matter also possesses wave-particle duality.
But the quantum weirdness doesn’t end here: If you were to measure the above particle at the location of the slits, it would “collapse” and proceed through only one of the slits as a classical particle would, apparently losing it’s wave-particle nature.
In historical hindsight, this of course happens due to a combination of the observer effect and quantum decoherence necessarily interacting (and thus changing) any quantum object measured. However, the specific mechanics of this collapse are still not totally agreed upon, which we call “the measurement problem.”
What is the measurement problem? What are quantum interpretations?
The measurement problem represents the difficulty of describing the specific mechanics of the wave function collapse, or even if it’s “collapsing” at all. Quantum interpretations are simply historical speculation about the measurement problem.
It’s important to note that understanding quantum interpretations is not required to understand modern quantum physics; much of this interpretive speculation is no longer valid anyway as new information and reasoning have come to the fore. In fact, QM and QFT are already some of the most accurate and successful theories in all of modern science. Although quantum interpretations are useful in their diversity in approaching the issue, they don’t fundamentally contribute to the theory, as they merely predict the same experimental outcomes from different philosophical perspectives. Unfortunately, a lot of nonsense and “quantum woo” is justified with these interpretations when in fact they are not part of the core science to begin with.
And while we’re on the subject of nonsense, I’d also like to dispel the notion that there’s anything magical about the collapse of the wave function. It’s simply an incompleteness problem: Although probabilistic, quantum theories are very much unitary in nature (meaning they evolve “forward” and “backward” in a causality-bound manner). They only become apparently non-unitary when you try to isolate them (which is the weird part we haven’t been able to figure out due to being physically prevented from measuring it; the measurement problem).
For example, the wave function collapse is a non-unitary byproduct of the wave function evolution suddenly interacting with the apparatus used to measure the collapse. The apparatus obviously must be in an eigenstate to be useful to us (even the smallest tools we could possibly design would be in an eigenstate). This means the quantum system is necessarily interacting with a classical system and any quantum behavior is very quickly averaged away via quantum decoherence, causing the apparent collapse.
The finer points of all this are still actively being debated by very smart people. It’s certainly possible that we may never reach a consensus agreement, as it’s not currently possible to test which quantum interpretation is “correct,” and that might or might not change. In my personal view, quantum interpretations certainly have their place as philosophical “sails” to help drive the progressive thinking and diversity of people working on quantum physics, but they are vastly overestimated in current importance by the general public.
What is quantum entanglement?
Here’s a definition from Wikipedia:
Quantum entanglement is a label for the observed physical phenomenon that occurs when a pair or group of particles is generated, interact, or share spatial proximity in a way such that the quantum state of each particle of the pair or group cannot be described independently of the state of the others, even when the particles are separated by a large distance.
If anything, quantum entanglement is very counterintuitive. It’s also quite real. Essentially, it’s the idea that entangled particles seem to instantaneously “know” what each other are doing, regardless of the distance between them (which seems to violate causality).
Here’s a solid description from the same article to further illustrate:
The paradox is that a measurement made on either of the particles apparently collapses the state of the entire entangled system—and does so instantaneously, before any information about the measurement result could have been communicated to the other particle (assuming that information cannot travel faster than light) and hence assured the “proper” outcome of the measurement of the other part of the entangled pair. In the Copenhagen interpretation, the result of a spin measurement on one of the particles is a collapse into a state in which each particle has a definite spin (either up or down) along the axis of measurement. The outcome is taken to be random, with each possibility having a probability of 50%. However, if both spins are measured along the same axis, they are found to be anti-correlated. This means that the random outcome of the measurement made on one particle seems to have been transmitted to the other, so that it can make the “right choice” when it too is measured.
The distance and timing of the measurements can be chosen so as to make the interval between the two measurements spacelike, hence, any causal effect connecting the events would have to travel faster than light. According to the principles of special relativity, it is not possible for any information to travel between two such measuring events.
What is the EPR paradox? Hidden variables theory?
Entanglement didn’t sit well with some respectable folks…
The EPR paradox was a challenge posed against the completeness of QM. It was a thought experiment proposed by physicists Albert Einstein, Boris Podolsky, and Nathan Rosen (EPR) in their paper Can Quantum-Mechanical Description of Physical Reality be Considered Complete?
The paradox argues that it’s possible to measure both the position and momentum of a particle simultaneously by setting up an experiment that measures two entangled particles from different observational axes, then sharing the findings to work out the missing information.
The argument was, if the uncertainty principle is to be maintained in this experiment, then entangled particles are either transmitting information to each other instantaneously (faster than light – violating special relativity and thus causality; Einstein called this “spooky action at a distance”), or there are “hidden variables” causing this action that we’re not aware of yet. I.e. quantum physics must be incomplete.
I recommend watching this video for a deeper understanding.
What is Bell’s theorem?
Bell’s theorem is math illustrating why hidden variables are not actually possible in the EPR paradox. It was later experimentally verified (meaning hidden variables has been proven false).
I recommend watching this video for a deeper understanding.
What are locality, non-locality, and realism?
- Locality is the idea that an object is directly influenced only by it’s immediate surroundings. For something to influence something else at a distance, there must be something between to mediate that action
- Non-locality is the opposite of locality, stating objects can be influenced by things beyond their immediate surroundings
- Realism in the context of quantum physics is essentially hidden variables theory. More broadly, it’s the implication that the Universe exists regardless of measurement or observation
For a long time, since the beginning of science really, we believed the Universe had “local realism.” However, quantum physics falsified locality on quantum scales due to entanglement, while Bell’s inequalities rule out local hidden variable theories – a form of realism that is compatible with locality. So we’re left with fundamental non-locality.
Interpretations of this counter-intuitive result are left to the “quantum interpretations” we covered above. I remind the reader that quantum physics works just fine without understanding any of this intuitively – it’s always important to remember that the Universe doesn’t care about whether it makes sense to us – it is what it is.
Lot’s of physicists simply accept these results, while many others are trying to resolve a deeper meaning in these experiments that is more appealing to our common sense.
What do I think?
This is just speculation from an amateur: I think quantum physics is indeed non-local, but only in one of two senses: It’s not non-local in the sense that information is being transmitted faster than light, which would violate causality. It is non-local in the sense that entangled particles share a statistical device (a shared wave function) and simply act as inverse mirrors of each other regardless of distance because they never stop being part of that single original superposition.
What this means is you and I can entangle two particles, then you can take your particle to the other side of the observable Universe. Once I measure my particle, I’ll instantly know what state your particle is in, which you can measure and confirm. I don’t know this because the two particles communicated in any way. Rather, I know this because the two particles simply shared the same statistical origin. No faster-than-light communication necessary.
The real question is how the wave function is sustained intact over large distances. Is there an intuitive explanation to the mechanics of the wave function collapse of entangled pair particles? I have no idea, thus the “measurement problem.”
What are virtual particles?
Quantum Field Theory treats particles as “excitations” of their underlying quantum fields (these excitations are also called “quanta”). Unlike a “real” particle, a virtual particle is a temporary excitation of this field. The longer the virtual particle remains, the more closely it resembles a “real” particle.
However, this is very misleading and confusing: Virtual particles are bound by the same hard physical laws of conservation that apply to everything else in the Universe and do not randomly pop in and out of existence. Rather, they are simply transformations of quantum states; there is no creation or destruction happening.
I like to think of virtual particles as residual environmental “noise” when you’re trying to isolate and measure a single quantum system. For example, if you’re trying to concentrate on what a single person is saying in a noisy crowd, just because you’re focused on that person doesn’t mean the crowd around that person is literally removed from existence. Virtual particles are kind of like the crowd, existing as temporary excitations (a kind of “noise”) surrounding the quantum system currently in focus.
Virtual particles can’t be measured directly with an experiment due to their nature and the uncertainty principle, but we deduced their existence from the math driving “perturbation theory.” They’re also used to explain something called the “Casimir effect.”
To summarize, “virtual” is a poor description of what a virtual particle really is (it’s debatable whether any English word accurately describes the concept). They are not being created and destroyed; they are simply the natural outcome of a quantum system changing over time and interacting with the environment.
What is quantum foam?
Quantum foam is the idea that spacetime itself is subject to the uncertainty principle, therefore it might fluctuate on the smallest scales, creating a sort of “foam” instead of being ”smooth“ as presented in classical physics. This idea exists because we don’t have quantum gravity pinned down yet. As long as that is the case, we can’t know what spacetime is like on the smallest scales.
What is zero-point energy (ZPE)?
ZPE has to do with how thermodynamics is suspected to work on quantum scales (I’ll explain thermodynamics in an upcoming post). Essentially, ZPE is the lowest possible energy a quantum system can have. It’s technically non-zero energy in principle, as quantum systems fluctuate constantly even at this theoretical lower limit. “Zero-point energy” is interchangeable with “ground state” or “vacuum energy” (in the case of space), but has a mathematical origin and sounds cooler so more people seem to use it.
Interestingly, ZPE has folks wondering whether a quantum aether exists (you can think of “aether” as the stuff between the stuff – a mediator of action; locality). Since the interpretation of this aether as a physical medium would contradict special relativity (causality), we can’t do that. It’s all quite confusing, really, because it ties into the quantum measurement problem and the issue of reconciling apparent quantum non-locality with everything else.
What is quantum gravity?
Quantum gravity is the idea that gravity is quantized. It’s an attempt at unifying quantum mechanics and general relativity, usually represented by the theoretical “graviton,” which hasn’t been discovered in any experiment to date.
QFT does practically well enough in unifying quantum mechanics and special relativity, but can’t account for gravity as outlined in general relativity. Currently QFT employs a kind of band-aid known as ”semiclassical gravity” to bridge the gap. Other theories like “string theory” and “quantum loop theory” also make attempts at integrating quantized gravity into the standard model, but there are serious outstanding problems and the science is ongoing.
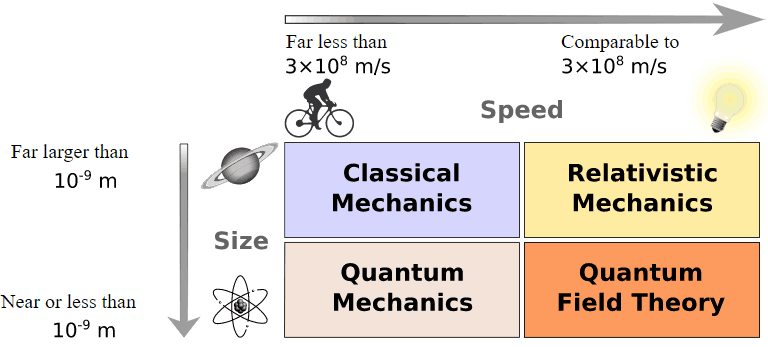
Did quantum physics replace classical physics?
No. If quantum physics is a scalpel, then classical physics is a hammer. The scalpel doesn’t replace the hammer, it’s simply a different tool better suited for another purpose.
Wikipedia produced the infographic below to give you a better sense of how these sciences are used:
Congratulations! You made it through my modern physics primers. I hope they were illuminating. 🙂
Sources: