Parting from mainstream physics, 26 year old Einstein took a leap of logic that the laws of nature should not apply only in certain situations, but in all situations. He postulated that the speed of light must be the same for all equal observers and then ran with that idea until it forced him to conclude that our understanding of time and space itself needed to be modified, essentially sweeping the rug out from under conventional physics.
Which is amazing for a 26 year old!
The results of all this upheaval is our modern understanding of space and time – relativity. And if you want to answer the deeper questions about the nature of our Universe, at least a rudimentary understanding of relativity is required. However relativity is admittedly a complex subject, which is why I’ve labored to distill it into a simple question and answer format for your convenience below.
There are three major themes we’ll want to explore – light, spacetime, and mass-energy equivalence.
We’ll start with light…
Light
Light is represented by the letter “c” in physics. It travels at 299,792,458 m/s (meters per second). This speed cannot be exceeded by anything with mass and is known as an “invariant constant,” meaning it never goes faster or slower than 299,792,458 m/s in a vacuum, regardless of reference frame.
This “invariant” speed is very important in physics. In fact, it happens to be a foundational pillar of Einstein’s theories of relativity (and much more). Everything obeys this “speed limit” – mass, energy, gravity, electromagnetic waves, everything. We use light to represent this invariant speed for historical reasons, but it just as easily could be represented by gamma radiation \gamma or even the speed that gravity itself propagates as gravitational waves.
Let’s dive into some deeper Q&A:
Why is light referred to as “c?”
The origin of “c” is ambiguous: Some folks think c began from the Latin word celeritas, which means “swift” or “speed.” It also conveniently implies c for “constant.” In reality, it’s tough to pin down a single origin, as c likely arose from a gradual consensus of many different scientists hopping on board the bandwagon and eventually deciding c is what we’ll all use to describe light.
How did we figure out the speed of light?
People have known light travels fast for a long time, we just didn’t understand the specifics. Many thought light was infinitely fast. Galileo was the first to try and put that notion to the test with an experiment in the early 17th century using lanterns, but he didn’t have the technology to successfully measure anything moving quite that fast so he had to give up.
The first successful test was conducted by Ole Römer in 1676 (by accident!) while he was studying Jupiter’s moon Io’s interaction with Jupiter’s shadow. Originally, he was trying to get a more accurate understanding of Io’s orbit. But as he made his observations throughout the year, he noticed that the time between when Io was in Jupiter’s shadow vs. when it was visible was changing based on how far away the Earth was from Jupiter. He realized the only logical explanation was that light travelled at finite speed. Using these delays, Römer and others then proceeded to calculate the speed of light with this new data remarkably accurately given the time period. Since then, we’ve refined that speed into the extremely precise measure we use today.
Why is light the speed it is?
No one really knows. The same is true for all Universal constants (light, gravity, causality, Planck’s constant, etc.) – it’s just the way things are. What we do know is that if these constants were altered in our Universe, stuff would break in horrendous ways.
In my personal view, it’s very probable that these Universal constants happen to be the only possible configuration of metrics that, when all interlocked, create a sustainably self-consistent and logically coherent Universe. So they are what they are because they have to be. We just haven’t completely gotten our heads around how to describe that mathematically yet.
Can we slow light down?
Only in an apparent fashion, but not fundamentally: If we direct light through a medium (like water, for example), we can make it seem to travel slower than it normally does in a vacuum. It appears to slow down because light literally scatters when it interacts with stuff. In fact, we use something called a “refraction index” to show how different materials have different scattering (“refractive,” technically) effects on light waves. Really what’s happening is light is a wave that is interacting with the constituent waves of the electromagnetic fields of the material it’s passing through, which has a slowing effect. We’ll talk more about waves and fields in the next primer on quantum physics.
For now, simply imagine light traveling in a straight line vs. through a maze. Obviously, due to the scattered direction of travel in mazes, there’s simply more distance to cover. That’s what’s happening in a nutshell. Interestingly, scientists have been able to run with this concept and slow light to human-comprehensible speeds by directing it through certain exotic materials that have really dense “mazes.”
What is mass?
When most folks think of mass, they’re actually thinking of “matter,” which is the stuff in the Universe. If you can touch it, it’s matter.
On the other hand, “mass” is a term in physics used to measure the properties of physical bodies (matter), namely their resistance to acceleration and causing of gravitational fields. Mass is simply a measurement and representation of the properties of matter.
What is rest mass?
For historical reasons, there are actually quite a few labels for mass – rest mass, inertial mass, gravitational mass (both active and passive), invariant mass, etc. They all have their place in physics, but really they’re all describing the same thing from different angles of interest – the various properties of the “stuff” out there.
Just like c, the magnitude of mass will not change from observer to observer. It is “invariant.” This is why in many physics lectures you’ll hear “mass is mass is mass is mass!”
Does an object’s mass increase as it approaches c?
No. This is confusion caused by the unfortunate term “relativistic mass,” which is no longer in use by informed physicists. An object’s actual mass isn’t changed due to its speed, but it’s inertial mass is.
Inertia is simply how difficult it would be to change the velocity of a moving object. Mass and speed influence inertia. For example, if a train and a bicycle are moving at the same speed, the train would be far more difficult to stop (difference in mass). Alternatively, a fired bullet would be much harder to stop than if you simply tossed that same bullet to someone (difference in speed). Inertial mass is what represents how hard it would be to stop or change these things if they were in motion, but the things themselves retain the same amount of mass as they had when they were motionless.
Why can’t light be outrun by anything with mass?
In modern physics, no object with >0 mass can ever travel at c. No object without mass can ever travel <c. Why is this? Well, increasing the speed of a massive object means increasing it’s inertia. In the everyday Earth environments we’re used to we don’t notice any unusual difficulty accelerating objects. But as you get closer and closer to the speed of light the inertia of the object you’re accelerating rapidly increases into infinity (this isn’t just a mathematical guess, it’s been experimentally verified extensively).
Remember, inertia is the tendency of an object to resist force. Since acceleration is inversely proportional to an object’s inertia and said inertia is increasing into infinity as you approach c, the difficulty of accelerating the object further is also increasing into infinity. Basically, it’s impossible to accelerate any object with non-zero mass to the full speed of light. In fact, it would take infinitely more energy than exists in the entire observable Universe to accelerate even a single proton to the speed of light!
Indeed, the fastest particle we’ve ever detected was the aptly named “Oh-My-God particle” discovered by the University of Utah’s “Fly’s Eye Cosmic Ray Detector.” This proton was moving at 9.99999999999999999999951%c. To provide perspective, if you placed a photon (packet of light itself) next to this proton and raced them, it would take the photon 215,000 years to get even a 1cm lead on the proton! And this wasn’t just a fluke either, we’ve detected particles moving at these speeds multiple times. Interestingly, we still don’t have a good explanation for their tremendous speed.
Yet, even the so-called “Oh-My-God particle” would require infinitely more energy to reach the speed of light, as hard as that is to comprehend.
Ok, but what would happen if something with mass actually exceeded c?
If you ask a physicist this question, you will likely get stonewalled with a lazy “nothing with mass can be traveling \geq c” response. The more empathetic answer is we simply don’t know, as your question doesn’t make logical sense given what we know about the Universe (meaning it’s impossible according to modern physics).
Any massive object would require infinite energy to accelerate to c, much less beyond it. Mathematically, you will get “imaginary” results when you mess with massive objects exceeding light speed in relativistic equations. For example, you’ll end up taking the root of a negative number, creating an imaginary number. This leads to causality-violating scenarios where you’ll have “imaginary time” and “imaginary space,” which doesn’t make any sense. This boils down to time not being an independent concept in the first place, thus you will never “travel” to/in/through it.
And while we’re on the subject of time, you’ll also no doubt hear the word “tachyon” randomly thrown about whenever “time travel” comes up, most notably in science fiction. Tachyons are theoretical particles that always travel faster than c. They have interesting properties like imaginary mass and weirdly speed up when they lose energy. Tachyons aren’t real in the sense that they’ve never been observed; there’s no evidence supporting their existence. Some folks only guessed they might be a thing because the concept of a tachyon coincidentally satisfies certain equations in relativity (but these types of false positives are very, very common in science, so take this with a pound of salt). The whole idea has been massively overblown by the media and most physicists don’t put any stock into tachyons because they break too many laws of physics. Most importantly, there’s simply no evidence of their existence.
What’s a reference frame?
A “reference frame” is basically a point of view. Think of you riding passenger in a car going a constant speed. As you look out the window, it feels like the world is moving backwards all around you while you are staying still. But from the reference frame of the pedestrians on the sidewalk, you are the one moving. Ultimately, everything has its own reference frame just like you in the car. There is no “absolute” frame of reference; all objects are in motion relative to each other.
Why is it called “relativity?”
In relativity, we notice striking differences in how I observe things in my reference frame and how you observe things in my reference frame from your reference frame at very high speeds or near strong gravity fields – i.e. how our observations relate to each other… “relativity.”
Spacetime
We’ve known about spacetime since long before Einstein was born. What he did that was so special is show how time isn’t the same for everyone and in fact requires its own coordinate system (dimension), leading to our modern understanding of four-dimensional spacetime. The real shocker was the counterintuitive discovery that both space and time can bend, yet are the same at all times – if you bend a coin, both sides are still part of the same coin. This means one person’s experience of time (and thus space) can be dramatically different than another person’s experience depending which reference frame you’re in (where you are on the coin).
To continue driving this point, here’s a classic analogy called the “twins paradox” (though it’s not really a paradox, as it’s very well-explained by special relativity): Say you have twins who grow up into identical adults. One of them decides to board a rocket ship capable of traveling at .99c. The rocket ship leaves Earth for a distant star 20 light years away. Unfortunately, the captain of the rocket ship forgot critical equipment back on Earth and they were forced to turn around just as they arrived at their destination (oh he was flogged, don’t worry). By the time the ship makes it back to Earth, the twin who left Earth has physically aged only 5.7 years while the twin who stayed behind has aged 40 years!
It turns out traveling faster through space actually compresses your time and length relative to other reference frames. The technical terms for this are “time dilation” and “Lorentz contraction,” respectively. Again, this is a real effect and has been measured in quite a large number of very accurate and heavily scrutinized public experiments.
Time for some Q&A:
Why can’t we observe these relativistic effects when we’re in a car or plane?
Because relativistic effects are imperceptible until you’ve reached a significant percentage of c. The speed of the fastest man made object as of this writing is the spacecraft Juno, which travelled at 0.00023c on its way to Jupiter. There’s a probe scheduled to be flown around the Sun that will be significantly faster but it won’t even break 0.1c, not even close. Light is mind-bogglingly fast.
Interestingly however, modern GPS satellites rely on high precision to function properly and thus must be calibrated to account for the tiny relativistic effects they experience relative to us on the ground as they orbit the Earth. They are a great example of a modern technology that wouldn’t work without understanding relativity.
Why does increasing speed contract time and length for the traveller?
Because in order for c to be conserved, spacetime has to bend when you move. And believe it or not, this happens because everything is actually always travelling at a constant speed c through spacetime!
It’s difficult to properly understand this relationship without using math, so here’s how it works: We exist in three spatial dimensions x, y, and z (length, width, and height, respectively) and one temporal dimension t (time). Light c is a constant number that the velocity v of these four dimensions summed must always be equivalent to, regardless of reference frame. For further simplicity, we’ll condense the three spatial dimensions into one variable space s with s=x,y,z. This relationship can be expressed with the following equation (which is oversimplified, as relativity is not linear, which is important to understand):
\Delta v_s \Delta v_t=c
The above illustrates an “inverse relationship.” That means space and time are perfectly connected dimensions in that their velocities are inversely proportional – if velocity increases in one, the other’s velocity must go down in order to preserve the constancy of light c, and vice versa.
In practice, this means if you are at rest relative to the observer, you are moving at light speed through the dimension of time (v_s=0, v_t=c). Alternatively, if you are moving near the speed of light through the spatial dimension, at say .9c, then the “velocity” of your time dimension will contract to c-.9c_s=v_t or simply .1c_t (your time will slow down relative to others, causing time outside your frame of reference to appear to “dilate”). Remember also that space contracts in the direction you are travelling in exact proportions to the contraction of the time dimension. Space is time and vice versa – “spacetime.” So to summarize…
As velocity through space increases \uparrow \Delta v_s, velocity through time decreases \downarrow \Delta v_t to preserve c, which means your time and spatial contraction increase, since t=s.
As velocity through space decreases \downarrow \Delta v_s, velocity through time increases \uparrow \Delta v_t to preserve c, which means your time and spatial contraction decrease, since t=s.
This isn’t the most intuitive relationship, but the bottom line is that c is always conserved regardless of what you do – move or stay still, it doesn’t matter. The deeper “why” behind this ultimately stems from the speed of light being a Universal constant, which I already addressed philosophically above – because it has to be.
I am driving my car at very near c and I turn on my headlights, what do I see?
Nice try! The answer is you would see nothing out of the ordinary. They would seem like ordinary headlights to you. However, observers in other frames of reference would notice your time and space have contracted proportional to how fast you are going, ensuring the light from your headlights (which is part of the spacetime you occupy) remained travelling at exactly c from their reference frame as well. Always and everywhere, c is maintained. You, along with your spatial and temporal experience of those headlights, would contract.
If c can’t be exceeded by anything with mass, then how are galaxies moving apart faster than c?
It’s true that distant galaxies are moving away from us faster than c (known as “Hubble’s Constant” H_0). However, locally (meaning in their immediate vicinity of space), these galaxies are moving at speeds well under light speed relative to their more immediate surroundings. What’s happening is that the space between things is “stretching” uniformly everywhere. This stretching is not noticeable over short distances, however it becomes very apparent over the truly enormous expanses of space.
This phenomenon occurs because the “stretching” effect of space is very weak when compared with the strength of gravity locally. However, beyond a certain distance, gravity loses too much strength and the stretching has an increasingly cumulative effect. This tradeoff causes galaxies to cluster locally, but drift apart if there’s sufficient space between them. Interestingly, this “drifting off” effect is accelerating, which is thought to be a result of the balance between “dark energy” and “dark matter” + gravity, which of course is a placeholder phrase for “we don’t really know what’s causing this effect yet.”
It’s important to note here that new space is not actually being created (space is already infinite), it is simply the metric of space itself between objects that is increasing. The Universe overall is expanding (as evidenced by red-shifting background radiation left over from the big bang), however we want to be careful about using the word “expand,” as it implies the Universe must expand into something else. That isn’t the case as we showed in previous premises – the Universe is infinite. There is no “edge” to the Universe, hard as that is to comprehend.
If the Universe is infinite and infinite light from infinite stars travels freely through space, then why is the night sky so dark?
Three reasons:
- Light has only been possible for about 13.8 billion years
- Very distant objects that emit light (and the light itself) are receding from us faster than the speed of light
- As light travels, it will eventually “red-shift” (expand its wavelength) beyond the visible spectrum
Interestingly, if you view the night sky through an instrument capable of seeing beyond the visible spectrum of light, it does glow.
Why is it called time “dilation” instead of time “contraction?”
Both are technically true, it just depends on which frame of reference we are referring to. Your time contracts if you are the one moving through space. But as you are moving, the time outside your frame of reference will dilate (expand) relative to your local experience of time.
Does relativity mean photons do not experience time?
Yes! Photons are really interesting. They don’t have rest mass and travel at c so their time is contracted infinitely (rendered zero relative to all other reference frames). This means that from the subjective perspective of the photon (inasmuch as subjective experience is even possible for a photon, which it isn’t technically) time does not exist; all of existence and all events ever are happening simultaneously around them (but cannot be said to have happened in the past or future because the photon’s speed is exactly c and not more of less).
Pretty nuts!
Even crazier is that photons don’t experience space, either (due to infinite Lorentz contraction). This means from their purely hypothetical subjective reference frame, photons are everywhere simultaneously (and possibly have size?) while from all other reference frames they are moving at c and have infinitely contracted (zero) size.
Why is time considered the 4th dimension if space and time are equal?
The short answer is “because math.” The long answer is that dimensions are simply a way to measure something. For example, the actual definition of the word “dimension” is simply “a measurable extent of some kind.” Arguably, temperature is just as valid a dimension as x and y are dimensions defining an area (width times length), or z a dimension defining height. We merely use the dimension of time to conveniently illustrate the paths of transformation taken by the three spatial dimensions, known as “Lorentz Transformations.”
The intuitive hole people dig themselves into occurs when they lump all dimensions into the same mental category, like dimensions being some other “space” that you can visit (I blame science fiction). In fact, dimensions are not “spaces” themselves, they are simple measurements of some specific attribute of existence. This means time is not the fourth dimension, it’s simply a convenient fourth dimension out of many potential fourth dimensions that most accurately helps us describe what’s going on. Again, time is merely an abstract measurement we invented to comprehend space. It isn’t a separate place you can go visit! Just like you can’t go visit a temperature, you can’t go visit a time!
Space can exist without time, but time cannot be said to exist without space (unless we use time t as an isolated abstract dimension purely mathematically, which in this particular case we would express as t=0. But that’s the same as saying temperature Kelvin k=0, which is “absolute zero” or the absence of temperature, temperature being simply the motion of particles. Interestingly, this also means t=0=k, which is incidentally a convenient description of the frozen Universe example I gave in the previous premise).
How would exceeding c violate causality?
It doesn’t really. At least, it’s not what people think. This is one of the more mind-bending questions in relativity and has to do with something called “simultaneity.” What makes this so unintuitive is primarily how we think about causality vs. the perception of causality (among other technical things like defining what “now” and “instant” mean to moving observers). The bottom line is causality is an absolute everywhere and always, but the perception of causality can genuinely be manipulated in faster-than-light (FTL) scenarios based on what reference frame you’re in.
Here’s an example scenario:
Figure 1:

A, B, and C above are observers on three planets equally distant apart in a straight line. Say by some magic you have a way to transfer a physical letter containing winning lottery ticket numbers from A to C via near-instantaneous FTL travel. It would look something like this:
Figure 2:

…Which makes intuitive sense. Everything looks normal and as expected the letter arrives at C before the light of it being written even makes it to B. But let’s add a traveler D moving at relativistic speeds and see what happens when we account for motion:
Figure 3:
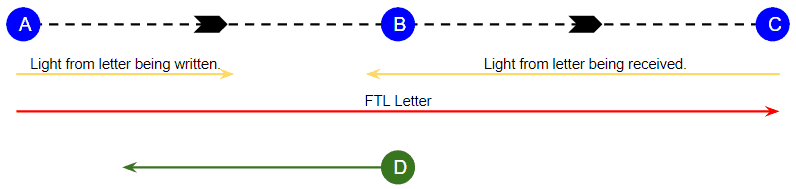
Remember, motion is relative and there are no absolute frames of reference. D is moving at relativistic speeds from the reference frame of the planets. However, from D’s perspective, D is the one standing still and the three planets are the ones moving past D. We’ll observe things from D’s reference frame here, which means the planets are the ones apparently moving.
Due to relativistic effects, D observes the light coming from A as moving slower relative to A. And even though the planets are equidistant apart, from D’s perspective, B will see the light from C before getting the light from A. This means from D’s frame of reference, B will appear to see the effect before the cause!
But the causality-preserving problem with this is B will disagree with D’s observation: From B’s perspective, nothing special has happened and B sees the light from A before getting the light from C (where C’s light is delayed by the FTL letter’s transit time), maintaining apparent cause and effect.
The key variables here are relative distance and speed. The further away and faster something is, the more apparent the skew to the one observing. However, no matter how far or how fast, the reality is one could never take advantage of the winning lottery numbers, because no true “backwards in time” causality violation has happened and it’s all essentially a relativistic mirage.
Ok, but what if we bounced the FTL letter between the planets and observer D in some clever fashion, could we create a scenario where A gets the letter before it is written? Nope. This is because traversing any distance never occurs in less than zero time (imaginary time is prohibited) and nothing massive can ever be accelerated c anyway. As long as that is the case, causality will remain an absolute of the Universe regardless of how you look at it – relativity does not violate causality.
It’s important to also note that lots of folks get confused here and misapply FTL in the above analogy: Serious FTL theories are not about breaking through the light speed barrier. Rather, they’re about finding loopholes such as bending space or traveling through wormholes. Basically, they’re about changing space and not about increasing speed beyond c. What this means is no matter how fast FTL is, instantaneous even, you’ll never travel in less than zero time, regardless of how you’re moving through space (wormholes, warping space, etc.). Time travel only applies when we’re referring to the former where something breaks through the light speed barrier, creating imaginary time; a sort of negative time where you could go back and literally talk to your past self. Again, this is impossible science fiction for all of the reasons we’ve covered.
The Universe simply doesn’t work in a way that allows for time travel; time travel and “temperature travel” are both equally nonsensical terms. Time and temperature are merely dimensions, which are measured attributes of space. You should be glad time travel is impossible too, as “temporal mechanics” would be a mind-bending nightmare of a science, not to mention the fact that if time travel machines went mainstream, some fool could accidentally (or even intentionally) prevent you from being born. Scary!
Mass-Energy Equivalence
Einstein also did something else that’s now crucial to our understanding of light – he showed how mass is equivalent to energy. More precisely, how E=mc^2, where E is energy and m is mass. Basically, mass is the same thing as energy…
Time for some Q&A:
What does the speed of light c have to do with mass and energy being the same?
This is a tricky question. E=mc^2 sounds like a simple equation, but it’s history is complex and it was worked out and refined by Einstein and others over many years. Describing the history of mass-energy equivalence could literally fill an entire chapter.
Simply put, the discovery of relativity led Einstein to conclude that because space and time are variable concepts in the Universe, many other physics equations are affected as well (this is why there’s a lot of relativistic equations that are required to describe different things – length contraction, relativistic momentum, relativistic energy, etc. Relativity shook up many areas of physics).
For example, this classical description of momentum:
p=mv
Became this relativistic description of momentum (which still behaves very similarly to the above equation at lower velocities, but accounts for relativistic effects at higher velocities):
p= \frac {mv}{\sqrt{1- \frac{v^2}{c^2}}}
As relativity was incorporated into other physics principles, it became mathematically apparent in relativistic environments (very fast speeds or around very intense gravity) that mass was having some kind of proportional impact on energy and vice versa. We just couldn’t see it before because the effects were too small at lower speeds (and we had no concept of relativity to guide us to that conclusion). Thus, E=mc^2 was eventually refined into existence through mathematical rigor and then later confirmed with experiments.
How do we know mass-energy equivalence is true, though?
In a word, nukes. Nuclear weapons technology came from actively studying the relationship between mass and energy. Nukes are “living” experimental evidence that mass, particularly fissile and fusile elements, are literally a highly concentrated form of energy that can be violently converted under certain circumstances.
Weirdly, the physics behind building a nuclear weapon are pretty straightforward. It’s the engineering and economics of it that make them so difficult to produce. But I’m not touching that with a ten-foot pole, thank you.
Does this mean the entire Universe is essentially just energy?
Yes, but it’s not that simple (alas, nothing ever is!). There is no such thing as “plain energy” or “pure energy” in the Universe. Those terms come from a misunderstanding of what energy really is. Energy is more like an adjective you use to describe the type of work being done. There’s no single type of energy that can perform every kind of work. For example, a magnet exerts magnetic energy. Magnetic energy isn’t general purpose energy – it will have a specific effect on iron shavings, but it will have no observable effect on materials like plastics. However if you physically kick a plastic bottle, you will kinetically transfer mechanical energy into it, which causes it to move.
A few examples of energy types out there:
- Mechanical: energy associated with motion transfer
- Electric: energy stored in electric fields
- Magnetic: energy stored in magnetic fields
- Chemical: energy due to chemical bonding
- Thermal: energy from the motion of particles (a kind of microscopic mechanical energy, actually)
- Nuclear: energy from the binding of electrons
- Rest: energy from an object’s rest mass (E=mc^2)
So now when you see those science fiction shows describing “beings of pure energy,” you’ll actively recognize these Hollywood types as the lazy, greedy ignoramuses they really are. Pure energy is not even a thing!
How can light have momentum if it has no mass?
This is a justifiably common question in physics. Classically, momentum is the product of mass and velocity. Here’s the equation again, where m is mass, v is velocity, and p is momentum:
p=mv
A photon does have momentum, but it doesn’t have mass. This is confusing as the two statements are clearly contradictory. How can p>0 if m=0 in the equation above? The best answer is the equation you’re looking at is not what it seems. m does indeed stand for mass, but that’s an antiquated way of calculating momentum (it originated around the time of Isaac Newton in the 17th century).
In modern physics, we’ve learned that momentum isn’t only about the motion of massive objects, instead it’s about the motion of stuff. For the sake of argument, if you replaced m with s for “stuff” you’ll see that light carries momentum. In fact, this agrees with experimental evidence where light has been shown to physically move objects – inside a radiometer, for example.
Photons may not have mass, but they are categorically “stuff” that exists in the Universe. It’s possible for stuff to carry energy, but not mass. A photon is an example of this. A photon carries energy inversely proportional to its wavelength and that energy is moving, thus it has momentum. Any stuff that has momentum (motion), massive or otherwise, can transfer that momentum into other objects as kinetic energy. I once again cite my radiometer example – photon “pressure” causes the panels on the radiometer to actually move.
Speaking of radiometers, in science-fiction you might have heard of “light sails” in space that use solar winds (light) as a form of propulsion between stars. This is where that idea came from!
What’s the difference between momentum and inertia?
This is another common question in physics I thought should be included here. The answer is simply that momentum is the quantity of motion, where inertia is the tendency for that quantity to stay as it is or “resist” change. If I throw a baseball, it has momentum because it’s in motion. The impact the baseball makes on the catcher’s mitt is due to inertia – the resistance of stopping the momentum of that ball.
Is gravity a force?
Yes. It’s one of the four “fundamental forces,” in fact. You’ll hear folks say it isn’t a force or that it’s a “pseudo-force,” but really the confusion is solely about semantics. Gravity is the mass or energy of objects causing changes in the motion of other objects. A force is defined as any interaction that changes the motion of an object. Can you spot the difference between those two sentences? I can’t!
Why does gravity weaken with distance?
You would think the answer is some deeper thing, but it’s actually a surprisingly simple idea that applies to many fields, including gravity.
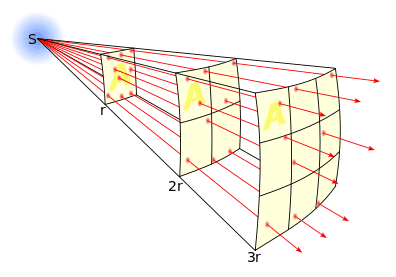
Simply, forces and fields weaken with distance because they are being diluted over a larger area. In physics, this is known as the “inverse-square law.” The intensity of gravity in this case is inversely proportional to distance squared. So for every unit of distance you travel away from the source of gravity, the strength of said gravity will decrease proportionally by that unit squared. So in the diagram above if you travel two units, gravity is \frac{1}{4} as strong, three units, gravity is \frac{1}{9} as strong, and so on. This is why the further you travel from Earth, the weaker its gravitational pull becomes.
Why does gravity bend space?
This is one of those questions where we can answer the “how,” but not the more fundamental “why.” We’ll start with a famous quote about the relationship in question:
Spacetime tells matter how to move; matter tells spacetime how to bend.
John Wheeler
Let’s recall that mass and energy are equivalent so you can think of matter (“energy” in this context) as basically everything we could potentially interact with in the Universe – planets, light, stars, electric fields, etc. – all are influenced by gravity. Essentially, energy “falls” towards it’s “geodesic,” which is a fancy word describing the natural path of energy through spacetime. Kind of like water flowing down a hill through the natural path of least resistance, energy will flow through spacetime along its geodesic.
Take another look at the John Wheeler quote above. That relationship is what actually defines gravity, but it’s tough to comprehend at face value, so we’ll have to break it down.
Matter (energy) tells spacetime how to bend: This is due to the “gravitational constant,” which is the quantified relationship between the geometry of spacetime (the bending) and energy as outlined in Einstein’s field equations. Basically, it’s what energy does to the space it occupies. More energy = more bending. No one knows why the gravitational constant exists (just as we don’t know the deeper why behind other Universal constants like c), just that it exists and how it influences things.
Spacetime tells matter how to move: If energy bends spacetime, then two objects next to one another will influence each other’s respective spacetime and thus each other’s geodesics. If the geodesic was a straight line when the object was alone, it will now be curved. The direction and “steepness” of that curve is proportional to the amount of energy present. More energy = more curvature. Both objects will then “fall” down their curvatures; their geodesics. The steeper the curvature of spacetime, the faster the fall (constrained by the speed of light, of course).
Consider an apple falling from a tree. Both the apple and the Earth curve spacetime and both fall along their geodesics. The apple’s geodesic is highly skewed towards the Earth’s tremendously greater energy, but the Earth’s geodesic is changed only an extremely tiny amount toward the apple (but it is changed). This causes the apple to “fall” in a parabolic geodesic toward the Earth. The Earth is technically falling towards the apple as well, but the change in it’s parabolic arc is imperceptible due to the vast differences in total energy. If we were to switch things up and cram the entire mass of the sun into the apple, then the Earth’s geodesic would be catastrophically affected and the Earth would immediately fall toward it’s new geodesic – almost directly towards the apple (which is now a black hole!).
What is a black hole, really?
Black holes come from stars. There are many different types of stars out there. The bigger ones turn into black holes eventually. They turn into black holes because bigger stars burn fuel faster. A star’s life cycle involves burning (fusing) hydrogen, then helium, then elements like carbon and oxygen, all the way down the periodic table until you get to iron. Iron doesn’t release energy like the previous elements, instead it consumes energy in aggregate. For this reason, once iron is being fused, a star is about to reach the end of its life.
A star is always in a tug of war between the expanding force of its heat energy (thermal pressure) and the contracting force of its gravity. Once iron is being fused, the amount of heat energy being produced drops off dramatically, meaning gravity dominates thermal pressure and the star begins to collapse very rapidly. However, this contraction actually causes a dramatic increase in thermal pressure due to this squeezing effect, ramping up internal fusion rates. Suddenly, this extra energy allows the star to fuse elements far beyond iron, even though this part of the periodic table consumes more energy than it produces, creating a runaway effect of massive proportions.
This all happens extremely fast and the result is an explosion of thermal force we know as a “supernova.” However as the supernova is occurring and the outer layers are blasted away into space, the core of the star may continue to collapse (if it’s big enough). As the core becomes more and more dense from the pressure on top of it, gravity skyrockets in the smaller and smaller volume of the core. This happens very quickly and the gravity at the core becomes so intense that nothing can resist it, not even light. At that point, you have infinite collapse, which is known as a “black hole.”
Black holes are fascinating objects. They’re permanently locked into a “frozen” or “infinitely collapsing” state of falling inwards due to extreme relativistic time dilation. The mass that was falling inwards has both enormous gravity and is traveling very near c. That means to all external observers of a black hole, time near a black hole appears to have slowed to a crawl. If you’re observing the event horizon itself, which is the boundary where not even light can escape, then time will have appeared to stop altogether. However, if you were to fall into the black hole yourself, time would feel normal to you. But the physical experience itself would be quite violent – the light around you would appear extremely warped and very rapidly you would be torn apart by gravitational tidal forces.
Interestingly, if you were to put a large star next to a black hole for comparison, you could actually travel much, much closer to the black hole without serious risk than you could with the star; many people dramatically overestimate the gravitational influence of black holes while underestimating the thermal influence of stars.
Is the speed of gravity the same as c?
Yes! Gravity does indeed propagate at the speed of light, as was shown by the gravitational waves emanating from the merging of two neutron stars labeled “GW170817” in 2017.
This is heavy speculation on my part and you should stop reading here if you know what’s good for you, but I find this to be interesting evidence of a potentially dual-nature of gravity: Since these waves were observed travelling so incredibly close to c that they might as well be exactly c, it’s logical to assume gravitons (the theoretical quantum elementary particles that make up gravity) are massless, yet attract mass, since c is conserved even on quantum scales. But then you have situations where singularities like black holes exist in the Universe, where not even light can escape. So why can gravity escape?
Unless…
What if gravity is actually multiple things that only look the same? We are perceiving a contradiction if we assume gravity is a singular concept – it can cause a singularity, yet escape a singularity. But if we break it into multiple concepts we might be able to explain this oddity. For example, let’s say we have two types of gravitons: “G-short” gravitons which are massless, attract mass, and obey spacetime geodesics. And “G-long” gravitons which are massless, attract mass, and disobey spacetime geodesics according to some parameter (I hate to use a science fiction term, but maybe they bypass conventional geodesics by travelling through some kind of “subspace?”).
These two (very) theoretical particles would shadow each other, giving the appearance of a singular concept, yet causing two seemingly contradictory outcomes – G-short gravitons would cause gravity as we conventionally understand it. G-long gravitons, perhaps emitted by G-short gravitons, would disobey spacetime curvature, allowing them to escape a singularity and travel over infinite distances as governed by the normal rules of gravitational physics, then somehow produce more G-short gravitons?
Interestingly, harnessing G-long gravitons would also allow for the possibility of FTL travel due to the potential of contracting the space in the direction they are emitted and riding space like surfing a wave, but that’s a whopper to tackle so we’ll put a bookmark in it.
Again, I’m just having fun here and this is wild speculation from an amateur. I’ve actually never gotten a straight answer to the question of how gravity, which evidently obeys the invariance of c and carries energy in waveform, can also escape a black hole. I suspect an explanation may not exist yet: Gravitons aren’t actually mentioned in special or general relativity, as they represent the quantized nature of gravity, which hasn’t been figured out yet. In fact, “quantum gravity” is pretty much the holy grail of physics right now and will be a major step in completing the framework describing our physical understanding of the Universe.
Speaking of quantum physics, is all of this clear as mud? Great, you’re feeling the same thing as every student of relativity ever! And it’s about to get a lot harder…
Sources: